1、先介绍一下什么是二项分布?二项分布就是重复n次伯努利试验。在每次试验中只有两种结果:yes or no,并且事件发生的概率p在每次试验中都是独立的。下图第一个公式是二项分布的公式,即进行n次试验,事件发生k次的概率分布。第二个公式是二项分布的期望,即进行n次试验,事件预期发生多少次。第三个公式是二项分布的方差,即进行n次试验,数据波动情况。

2、下面用MATLAB演示二项分布。例如A队每次赢球的概率p=0.7,现在进行了20次试验(比赛),求A队赢球的二项分布淌捌釜集X~B(20, 0.7)。启动MATLAB,输入以下代码:close all; clear all; clcn = 20; % 20次试验p = 0.7; % 事件A发生的概率为0.7q = 1-p; % 事件A不发生的概率为1-pf = zeros(1,n+1); % 对二项分布f赋予初值for k=0:1:n; % 事件A发生k次,求二项分布f,即成功k次的概率 f(k+1) = (factorial(n)/factorial(n-k)/factorial(k))*p^k*(1-p)^(n-k);endbar(0:n,f);hold onplot(0:n,f,'y-','LineWidth',3);hold off其中factorial(n)是求n的阶乘,(factorial(n)/factorial(n-k)/factorial(k))其实就是C(n,k)的意思。
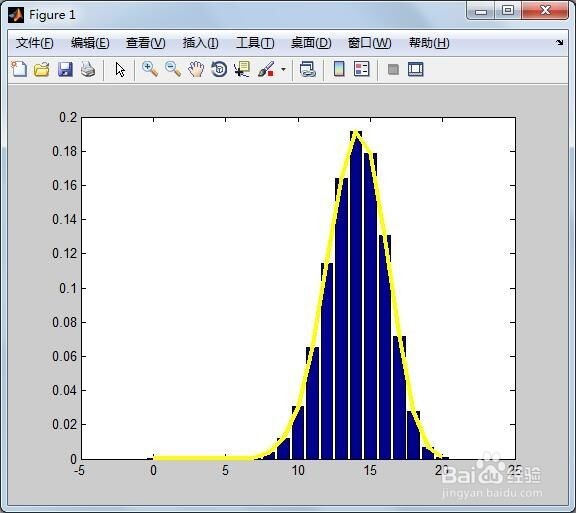
3、保存和运行上述代码,得到如下图形。可以看到该二项分布B(20,0.7)在20次试验(比赛)中,事件A发生(A队赢球)最多的次数是14。其实通过计算期望np=20*0.7=14,我们也可以知道,在20次比赛中,事件A发生(A队赢球)预期发生14次。
4、如果把事件A的发生的概率改为p=0.5,再次运行上述代码。
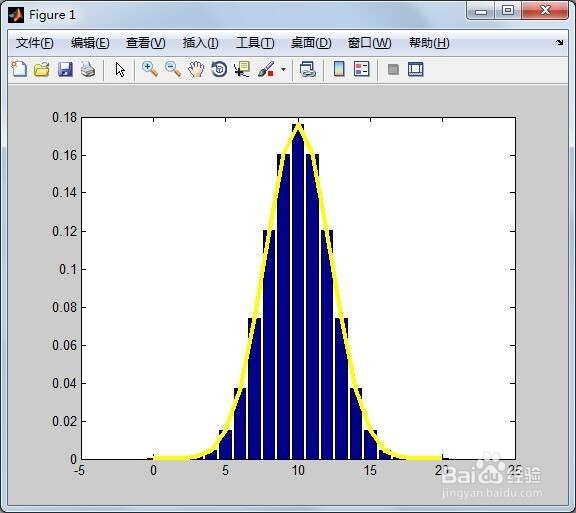
5、从下图可以看出,当p=0.5时,得到的二项分布,与正态分布接近。
6、在命令行窗口输入sum(f),计算20次试验中,事件发生k次的概率之和,可以发现它等于1。也就是说,n次试验中,事件发生k次的概率之和为1.
