一条线可以把一个面分成两部分,两条线相交可以把面分成四部分,三条线两两相交可以把面分成七部分。n条直线两两相交可以把一个平面分成(n(n+1)/2)+1部分。将四带入可以十一。
所以只要四条直线中的任意两条均在圆内相交即可分成十一个格子。示例如下:
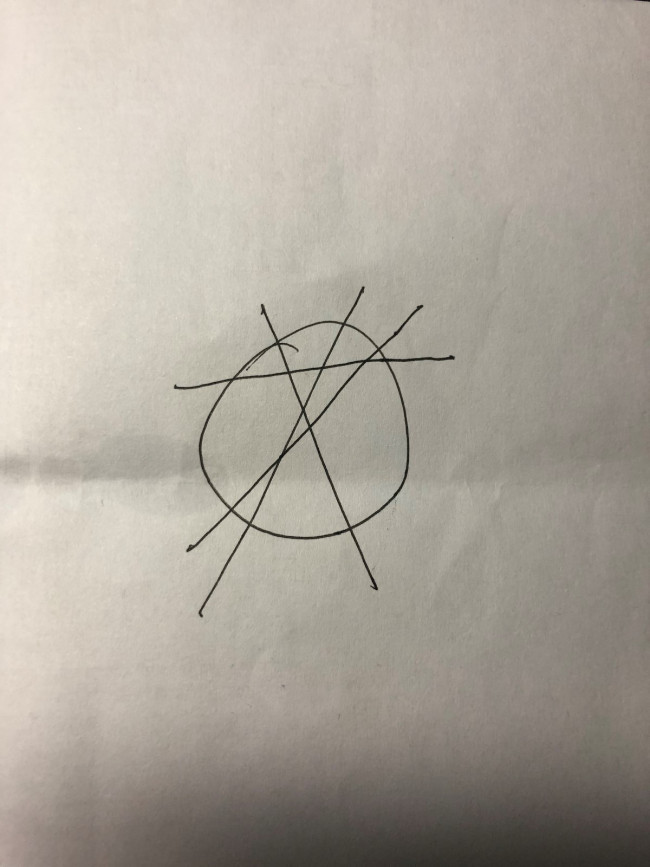
扩展资料:
直线分面公式的推导过程:
如果没有一条直线,那么平面就可以看作1个部分;如果有1条直线,那么平面就被分成2个部分。
如果有2条直线,又可分为两种情况:第2条直线与第1条直线不相交,可分平面3部分,第2条直线与第1条直线相交,可分平面4部分。
同理,3条直线最多可分平面7部分,4条直线最多可分平面11部分,再把这几个数分解,发现1=1,2=1+1,4=1+1+2,7=1+1+2+3,11=1+1+2+3+4。
由此我们可得到直线分平面公式:n条直线最多能把平面分成1+1+2+3+……+n个部分,即最多能把平面分成(n(n+1)+2)/2个部分,化简以后为(n^2)/2+n/2+1。